Aborder la géométrie plane dès le CE2 est un pilier essentiel du programme scolaire, permettant d’établir les fondements de l’abstraction spatiale chez l’élève. Au cœur de cette discipline se trouve le triangle, une figure géométrique de base dont la maîtrise est cruciale pour le développement des compétences mathématiques. À ce stade de l’apprentissage, l’objectif est d’amener les enfants à comprendre et à manipuler avec assurance le triangle équilatéral, d’en calculer le périmètre et d’appréhender la notion des angles, notamment les angles triangles opposés. Une approche didactique ajustée assure l’adaptabilité de la leçon à leur niveau de compétence, tout en répondant à l’intention des utilisateurs en quête de leçons structurées et efficaces pour leurs enfants.
-
Leçons, trace écrite, cours de la catégorie Le triangle : CE2, pdf à imprimer, fiches à modifier au format doc et rtf.
Leçon Le triangle : CE2
Principaux objectifs travaillés
Connaître le vocabulaire du triangle.
Identifier un triangle dans une figure complexe.
Connaître les triangles particuliers et leurs propriétés.
Savoir nommer un triangle.
Identifier les triangles – Ce2 – Leçon – PDF à imprimer
Paru dans ▶ Leçons - Le triangle : CE2
Lié à la séquence ▶ Identifier les triangles – Ce2 – Fiche de préparation
Lié à la séquence ▶ Identifier les triangles – Ce2 – Fiche de préparation
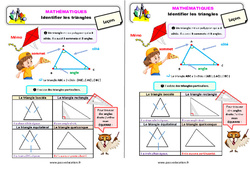
Retrouvez la leçon sur “Identifier les triangles” au Ce2 ❶ Un triangle est un polygone qui a 3 côtés. Il a aussi 3 sommets et 3 angles. ❷ Il existe des triangles particuliers. Le triangle isocèle Le triangle rectangle Il a deux côtés égaux. Il a un angle droit. Le triangle équilatéral Le triangle quelconque Il a trois côtés égaux. Il n’a aucune particularité. Pour trouver des angles droits j’utilise mon ÉQUERRE ! Voir les fichesTélécharger les documents Leçon…
-
Le triangle : CE2 - Leçon
Développement des compétences en géométrie : le triangle équilatéral, périmètre et angles
Le triangle équilatéral : définition, propriétés et méthodes de reconnaissance
L’exploration de la géométrie plane conduit inéluctablement au triangle équilatéral, une figure symétrique dont les trois côtés présentent une égale longueur. Lorsque l’on évoque ses propriétés, il convient de souligner non seulement cette équité dimensionnelle mais aussi les angles, implacablement identiques, mesurant chacun 60 degrés. Les élèves de CE2 apprennent à le tracer avec précision, en s’aidant d’une règle et d’un compas, outils qui incarnent la rigueur et la précision géométriques.
Calcul du périmètre d’un triangle : formules et cas spécifique de l’équilatéral
Le périmètre d’un triangle est obtenu par la somme des longueurs de ses trois côtés. Pour le triangle équilatéral, cette opération se simplifie, car il suffit de tripler la mesure d’un côté pour obtenir le périmètre total. Ainsi, si un côté mesure 5 cm, le périmètre sera de 15 cm.
Compréhension et calcul des angles dans les triangles
Les angles des triangles recèlent des subtilités qui fascinent les géomètres en herbe. Les angles opposés n’existent pas à proprement parler dans les triangles, mais dans des figures comme les quadrilatères. Cependant, il est essentiel de comprendre que dans un triangle, la somme des angles est toujours égale à 180 degrés, une constante qui offre un cadre rassurant à l’esprit des élèves.
- Définition d’un angle
- Propriétés des angles dans les triangles
- Importance de la somme des angles dans les résolutions de problèmes
Cette compréhension des angles est d’autant plus cruciale lorsqu’elle est appliquée aux propriétés des triangles équilatéraux, dont les angles sont toujours congruents, révélant une harmonie qui est à la fois mathématique et esthétique.
Exploration du triangle équilatéral
Qu’est-ce qu’un triangle équilatéral exactement ?
Un triangle équilatéral se définit par sa symétrie parfaite : ses trois côtés affichent la même longueur et ses angles internes, identiques, mesurent chacun 60 degrés. Cette égalité des mesures le distingue des autres formes de triangles, comme le triangle isocèle ou le scalène, et lui confère des propriétés géométriques uniques exploitables dans diverses applications pédagogiques.
Comment s’y prend-on pour calculer le périmètre d’un triangle ?
Le périmètre d’un triangle s’obtient en additionnant la longueur de ses trois côtés. Pour le cas particulier du triangle équilatéral, le calcul se simplifie : il suffit de multiplier la longueur d’un côté par trois. C’est une formule facile à mémoriser pour les élèves de CE2, leur permettant d’aborder avec confiance des problématiques géométriques plus complexes.
En quoi les angles opposés sont-ils particuliers dans les triangles ?
Chaque angle dans un triangle a une relation spécifique avec les côtés opposés. Au sein d’un triangle équilatéral, tous les côtés étant égaux, les angles opposés le sont également, renforçant ainsi l’homogénéité de cette figure. Cette particularité offre un cadre robuste pour l’enseignement des concepts fondamentaux de la géométrie plane aux élèves du CE2.
